2023-01-04

Polynomial Commitment Benchmark

$\gdef\F{\mathbb{F}} \gdef\G{\mathbb{G}} \gdef\Commit{\mathsf{Commit}}$

It is hard to compare complete proof systems because they have wildly different designs and implementing a balanced suite of benchmarks that shows what each is capable of is an enormous amount of work.

$🍎 ≟ 🍏$

But all proof systems use some form of polynomial commitment. These take a vector $\vec y ∈ \F^n$ representing a polynomial $P(X) ∈ \F[X^{<n}]$ evaluated on some domain (usually typically of unity) and turn it into a small commitment object, a process called $\Commit$ . I will ignore the $\mathsf{Setup}$ , $\mathsf{Open}$ and $\mathsf{Verify}$ processes as they are amortized over many or large proofs. (Though $\mathsf{Open}$ is a significant factor, and so is witness generation, and lookup, and ...)

Implementations

I picked the following libraries to benchmark, and for each library I picked what I assume are the highest performing parameters. Assembly code, multithreading and other speed improvements are enabled where optional. I'm ignoring zero-knowledge, proof size and verification cost as all of that can be taken care of with a layer of recursion.

blst Not a ZKP framework, but can be used to implement KZG.
gnark A comprehensive Groth16 and Plonk framework from Consensys.
halo2 ZCash's Plonk framework using inner product arguments (IPA).
pse Halo2 fork with KZG support from the Ethereum Foundation and Scroll.
plonky2 Goldilocks-FRI Plonk with efficient recursion from Polygon Zero.
ark The Arkworks comprehensive library for ZKP development.
winter Facebook Winterfell as used by Polygon Miden.
risc0 A tiny field FRI for a RiscZero's RISC-V zkVM.

$\begin{array}{lccccc} & \text{Algo} & \F & \ceil{\log_2{\vert \F \vert}} &\text{Hash} & R^{-1} & \text{Add} \\[0.7em] \texttt{blst} & \text{KZG} & \text{BLS12-384}\ \G_1 & 255 & & & ✓ \\[0.4em] \texttt{gnark} & \text{KZG} & \text{BN254}\ \G_1 & 254 & & & ✓ \\[0.4em] \texttt{halo2} & \text{IPA} & \text{Pallas} & 255 & & & ✓ \\[0.4em] \texttt{pse} & \text{KZG} & \text{BN254}\ \G_1 & 254 & & & ✓ \\[0.4em] \texttt{ark} & \text{KZG} & \text{BN254}\ \G_1 & 254 & & & ✓ \\[0.4em] \texttt{plonky2} & \text{FRI} & \text{Goldilocks} & 64 & \text{Keccak} & 2 & \\[0.4em] \texttt{winter} & \text{FRI} & \text{f62} & 62 & \text{Blake3} & 2 & \\[0.4em] \texttt{risc0} & \text{FRI} & \text{Fp} & 32 & \text{Sha256} & 4 & \\[0.4em] \end{array}$

In the table if $\F$ is an elliptic curve, then its scalar field is implied. A check under $\text{Add}$ means the commitments support additive homomorphism, this means that given $\Commit(P)$ and $\Commit(Q)$ we can compute $\Commit(a⋅P + b⋅Q)$ . For FRI implementations the rate $R^{-1}$ is set to the lowest supported, trading off proof size for better prover time.

For the KZG and IPA algorithms the $\Commit$ computes a multi-scalar multiplication (MSM, a.k.a. multi-exponentiation). For FRI it interpolates the polynomial using number-theoretic transforms (NTTs, a.k.a fast-fourier transforms) and then computes a Merkle tree.

To do. Add barettenberg and rapidsnark (both KZG over BN254) and an Orion implementation like this one.

https://github.com/starkware-libs/ethSTARK https://eprint.iacr.org/2021/582.pdf https://twitter.com/EliBenSasson/status/1610724082173235200

Machines

m1-max M1 Max Macbook Pro with 64GB memory and 2+8 ores.
hpc6a AWS EC2 instance with 370GB memory and 96 cores.
a15 Apple iPhone 13 Pro with 6GB memory and 4+2 cores.

Given that the primary use case of ZKPs right now is R&D, the most common hardware is a Macbook Pro. For real world privacy use cases the phone is much more important, and for computational integrity the server hardware is relevant.

To do. An x86_64 based desktop and arm32 phone. And gpu and wasm targets.

Results

Graphs show $\Commit$ throughput in field elements per second for increasing numbers of elements. Starting with the Macbook:

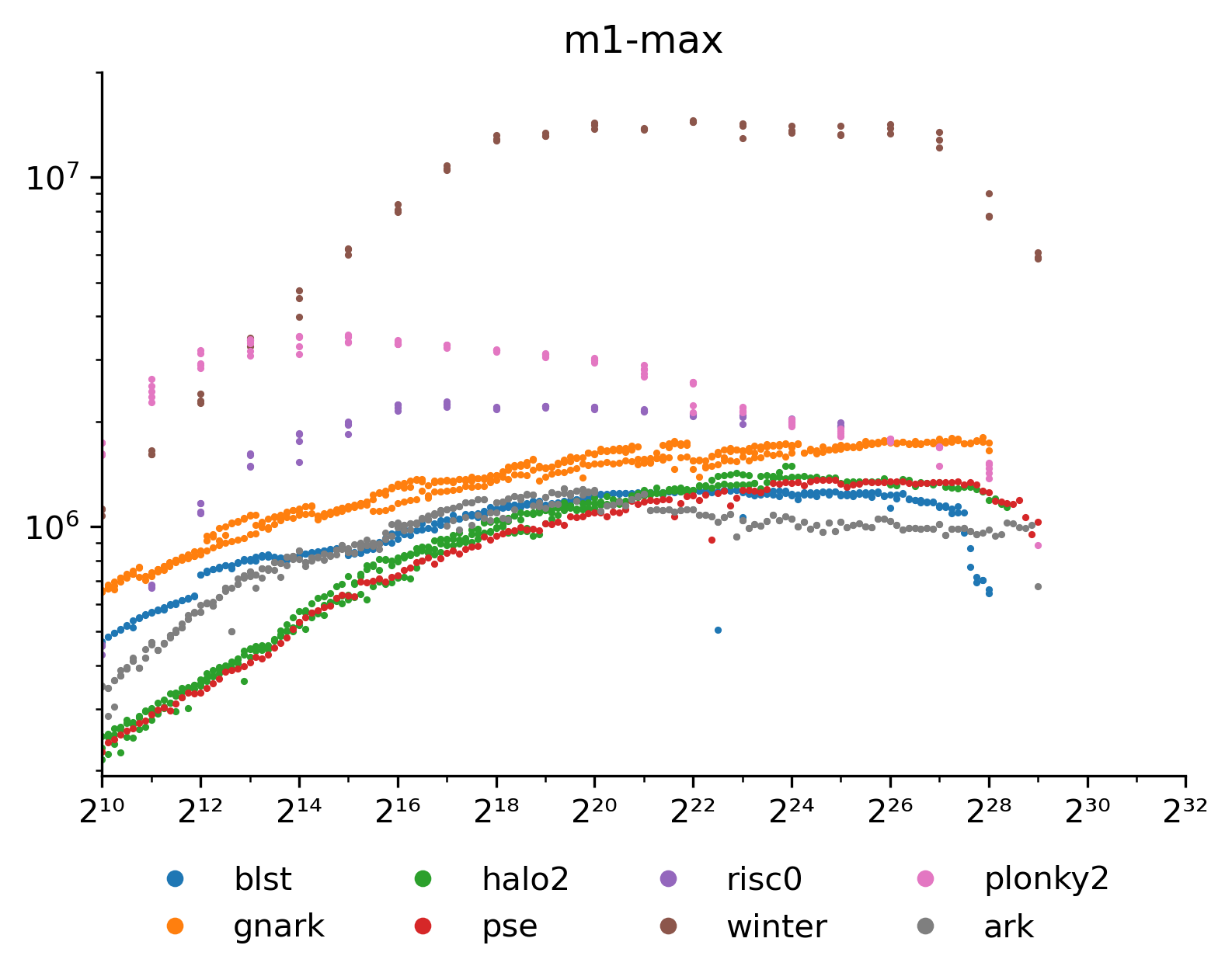
All the MSM based commitments run within a factor two of each other once we hit an initial scale of $~2^{16}$ . The FRI based commitments do considerably better, with Winterfell processing elements 10x faster. All of them run out of memory around $2^{28}$ to $2^{29}$ elements, except Risc0 which hits its theoretical limit at $2^{25}$ .

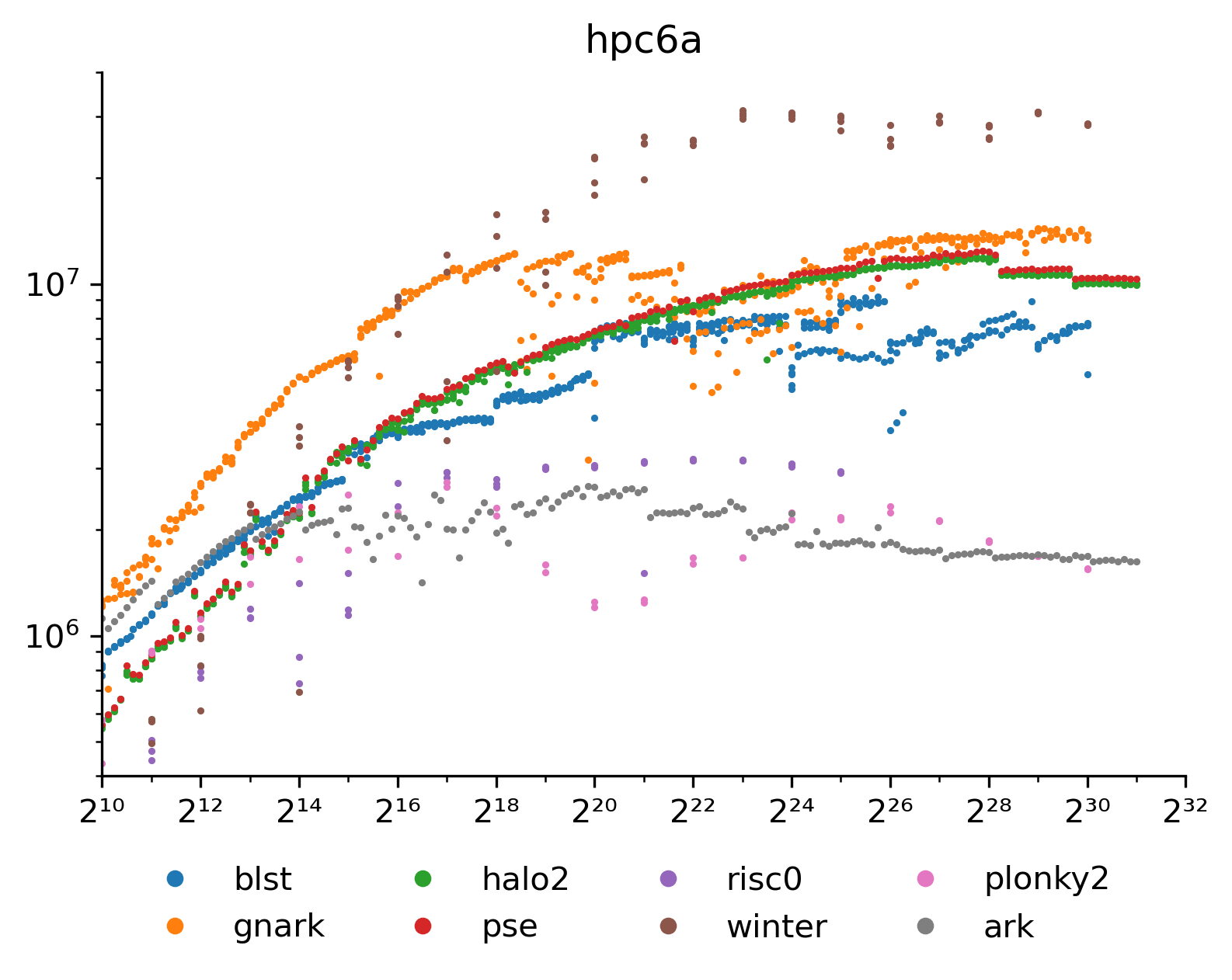
With $10\times$ more cores parallelization becomes critical. Plonky2, Risc0 and Arkworks struggle with this and perform equal or worse than before. Most of the MSMs get the expected $10\times$ boost, but the spread is a bit larger. The Halo2 forks have surprisingly consistent performance. Gnark seems particularly good at picking up the cores (or perhaps it is more optimized for x86). Winterfell still performs excellent but only $2\times$ instead of $10\times$ better. Like the other FRIs it also struggles with parallelization. The $5\times$ extra memory translated well to $4\times$ larger commitments.

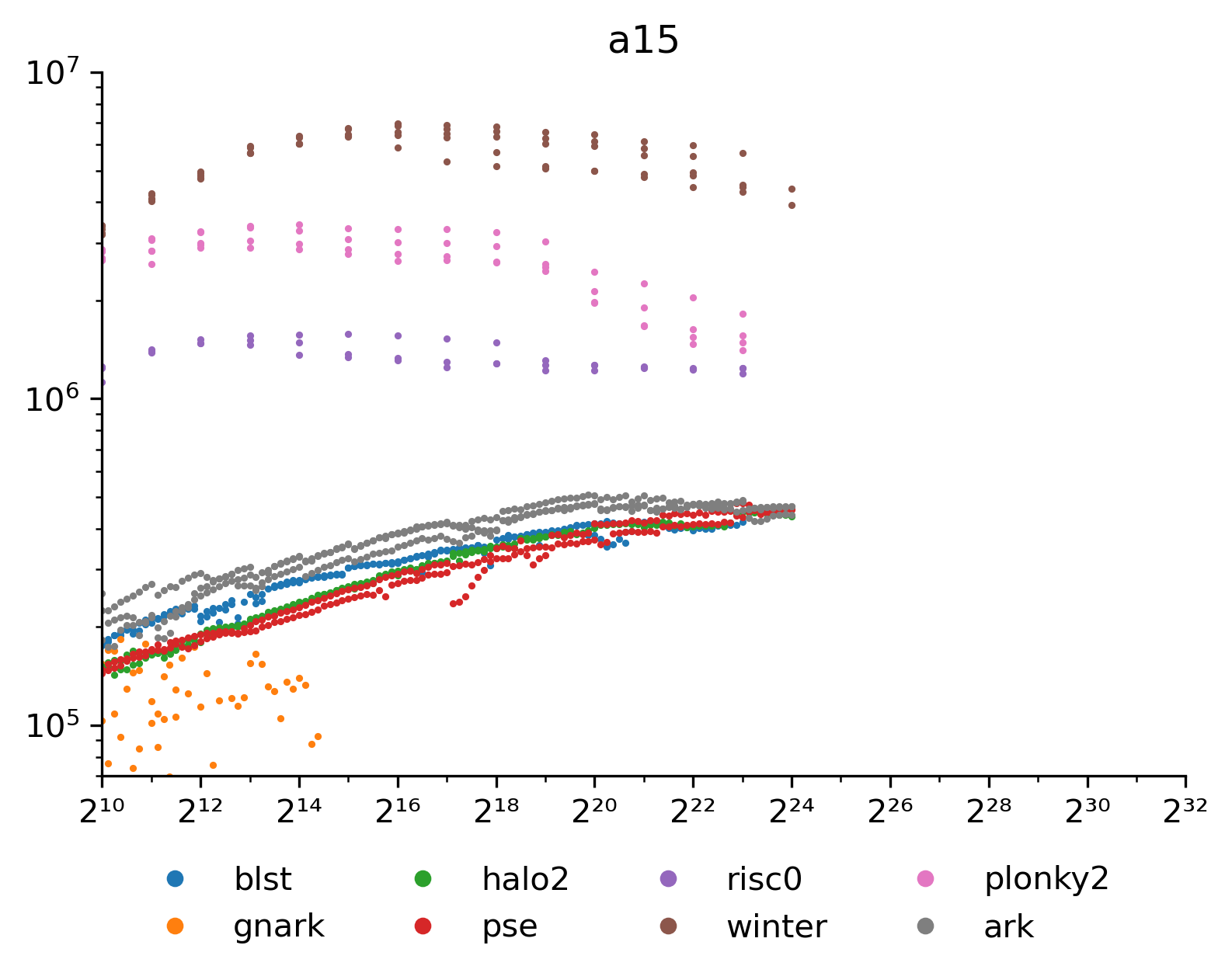
On phones the memory was very constraint. Despite $6$ GB memory being available iOS terminates processes using more than $2$ GB. This limits commitments to about $2^{24}$ elements. The phone also slows down slightly as its casing approaches $40\degree\rm{C}$ , which shows up as inconsistent performance for all the algorithms.

I don't know what is up with Gnark here, it drops out of scale and fails at $2^{16}$ . Either the code from winning the mobile ZPrize has not been upstreamed yet or my gomobile setup is wrong. The Gnark performance there was $2^{16}$ elements in $0.569$ seconds or $115\ \text{kElement/s}$ on a 6+2 core processor.

Limits

For all these implementations there is a theoretical limit to size determined by the availability of power-of-two roots of unity (at least for Stark and Plonk arithmetization). For BN254 and risc0 this limit is lower and practically reachable. For the rest we run out of memory before we get there.

$\begin{array}{ll} & \texttt{a14} & \texttt{m1-max} & \texttt{gpc6a} & \text{limit} \\[0.7em] \texttt{blst} & 23 & 28 & 30 & 32 \\[0.4em] \texttt{gnark} & 16 & 30 & 30 & 28 \\[0.4em] \texttt{halo2} & 24 & 28 & 31 & 32 \\[0.4em] \texttt{pse} & 24 & 29 & 31 & 28 \\[0.4em] \texttt{plonky2} & 23 & 28 & 30 & 31 \\[0.4em] \texttt{ark} & 24 & 29 & 31 & 28 \\[0.4em] \texttt{winter} & 24 & 29 & 30 & 31 \\[0.4em] \texttt{risc0} & 24 & 25 & 25 & 25 \\ \end{array}$

Conclusion

The FRI based algorithms perform excellent on smaller machines, despite being $O(n⋅\log n)$ versus $O(n)$ for MSM. The asymptotical performance is moot because memory issues dominate well before the asymptotes come into play. Winterfell consistently performs best for larger commitments.

It is surprising that the FRI algorithms run out of memory around the same time as the elliptic curve ones, despite the input size being $12\times$ smaller. This can be partially explained by extra allocations for the low degree extension and the Merkle tree.

Less surprising is that the FRI algorithms make ineffective use of multiple cores, with Winterfell only performing $2\times$ better with $10\times$ more cores. Number theoretic transforms are notoriously hard to parallelize.

Gnark looks exceptional among the elliptic curve solutions, it is unfortunate that did not perform well on mobile.

Source code for the benchmarks at recmo/pc-bench.