Goldilocks Reduction
\gdef\delim#1#2#3{\mathopen{}\mathclose{\left#1 #2 \right#3}} \gdef\p#1{\delim({#1})} \gdef\abs#1{\delim\vert{#1}\vert} \gdef\F{\mathbb{F}} \gdef\mod#1{\delim[{#1}]} \gdef\floor#1{\delim\lfloor{#1}\rfloor}
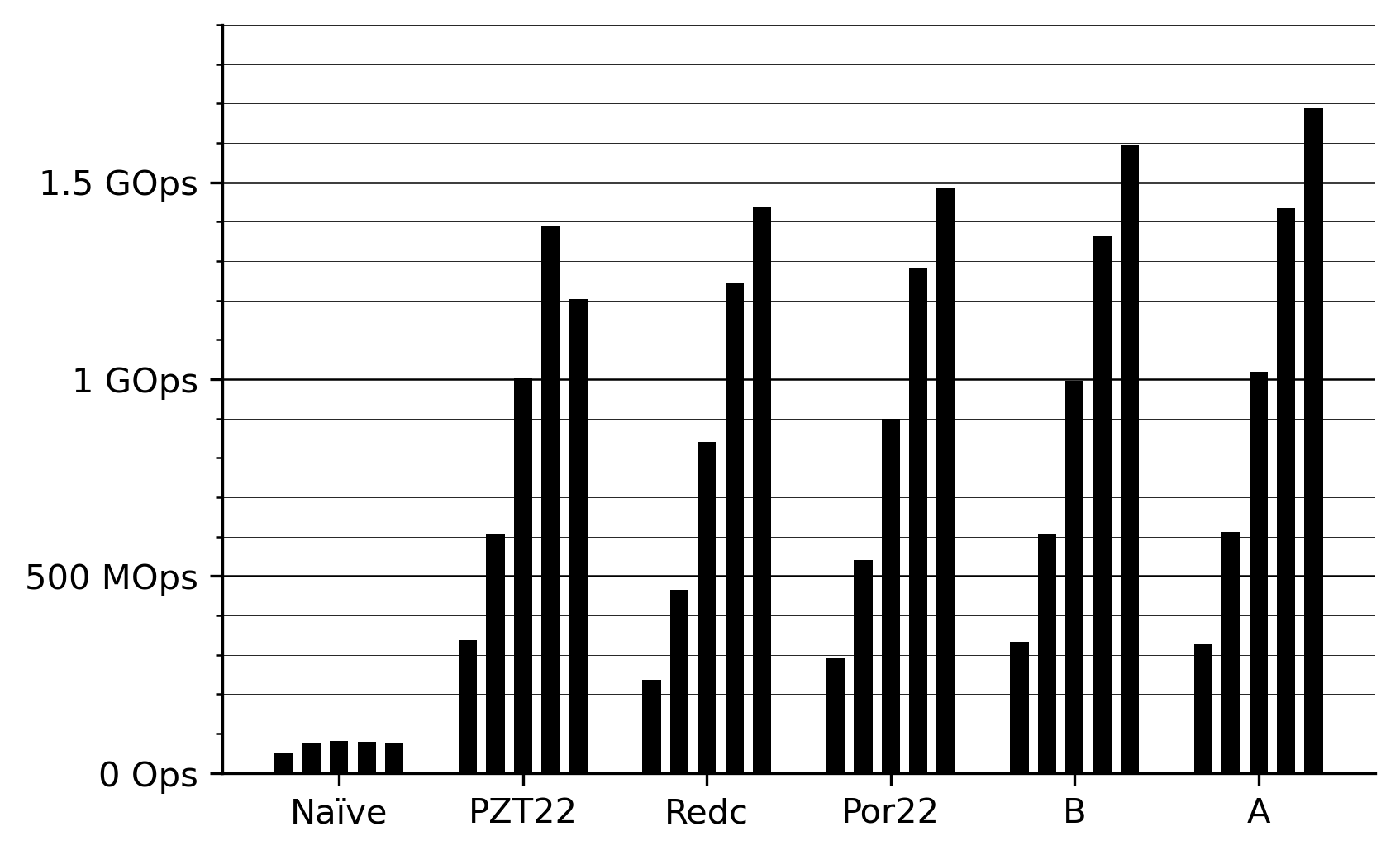
The goal is to compute \mod{a⋅b}_p where p = 2^{64} - 2^{32} + 1 is the Goldilocks prime and a,b∈[0,p) (or some suitable alternative for multiplication in \F_p). I've benchmarked existing methods and present a new method with variants A and B. Unfortunately these don't work in all cases.
\begin{array}{llllc} & \text{Algorithm} & \text{Input} & \text{Output} & \text{Portable} \\[0.7em] \texttt{Naïve} & \text{Knuth} & [0,2^{128}) & [0,p) & ✓ \\[0.4em] \texttt{PZT22} & \text{Direct} & [0,2^{128}) & [0,2^{64}) & \\[0.4em] \texttt{Redc} & \text{Montgomery} & [0,2^{64}⋅p) & [0,p)⋅2^{-64} & ✓ \\[0.4em] \texttt{Por22} & \text{Montgomery} & [0,2^{64}⋅p) & [0,p)⋅2^{-64} & ✓ \\[0.4em] \texttt{B} & \text{Barrett} & [0,2^{128}) & [0,2^{64}) & \\[0.4em] \texttt{A} & \text{Barrett} & [0,2^{64}⋅p) & [0,2^{64}) & ✓ \\[0.4em] \end{array}
The benchmark measures the number of multiply-reduce operations-per-second (Ops) on a single 3.2 GHz M1 Max Firestorm core with N-way instruction-level parallelism for N∈\set{1,2,4,8,16}. The measured code is
for _ in 0..iters {
for i in 0..N {
a[i] = mul_reduce(a[i], b[i]);
}
}
where N is compile time constant and a, b are [u64; N] are initialized with random elements from [0,p). I confirmed that the compiler inlines and unrolls the inner loop. The outer loop iterates a variable number of times and is used by Criterion to measure the code.
Benchmarking these functions is challenging because they take only a few nanoseconds. Some variants have branches so we need to feed them 'fresh' numbers each time to make branch prediction realistic. we also need to create data dependencies to force at most N-way parallelism. There is likely a non-trivial measurement overhead, but this should be the same for all methods.
Methods
Naïve approach
Let's do the dumb thing first:
const MODULUS: u64 = 0xffff_ffff_0000_0001;
fn mul_naive(a: u64, b: u64) -> u64 {
((a as u128) * (b as u128) % (MODULUS as u128)) as u64
}
The naïve implementation looks simple, but the generated instructions are not. There is no suitable native instruction so the compiler (LLVM) generates a call to the __udivmodti4 compiler built-in function, which implements Knuth division. It is slow because it is generic and does no preprocessing on MODULUS.
For 64-bit reductions there is the UDIV instruction, but this instruction is funny in that it takes either 7, 8 or 9 cycles. It is the only one with variable cycle count! So even the silicon is doing some sort of loop. Fortunately for 64-bit LLVM is smarter and it turns a 64-bit a % MODULUS into a conditional subtraction. But as noted by PZT22, it's actually faster to use a branch here.
Direct reduction
\mod{x}_p = \mod{x_2⋅2^{96} + x_1⋅2^{64} + x_0}_p = \mod{x_2 ⋅ \p{-1} + x_1 ⋅ \p{2^{32} - 1} + x_0}_p
This method expands the number in base 2^{32} and uses the particularly simple reductions of powers of this base in Goldilocks to reduce the number. This is the method in Gou21 and Plonky2 uses a heavily optimized version presented in PZT22 that reduces to [0, 2^{64}):
fn mul_pzt22(a: u64, b: u64) {
const EPSILON: u64 = (1 << 32) - 1;
let x = (a as u128) * (b as u128);
let (x_lo, x_hi) = (x as u64, (x >> 64) as u64);
let x_hi_hi = x_hi >> 32;
let x_hi_lo = x_hi & EPSILON;
let (mut t0, borrow) = x_lo.overflowing_sub(x_hi_hi);
if borrow {
branch_hint();
t0 -= EPSILON;
}
let t1 = x_hi_lo * EPSILON;
let (res_wrapped, carry) = t0.overflowing_add(t1);
res_wrapped + EPSILON * (carry as u64)
}
where branch_hint() is an empty volatile function forcing the compile to use a branch instead of conditional instructions. Plonky2 has another clever trick in x86_64. This does not translate directly to Aarch64 because the carry flag behaviour is different, but we can achieve the same using csetm w9, cs. To use it replace the last two lines with this assembly:
adds x8, {t0}, {t1} ; x8 = t0 + t1 (setting carry flag)
csetm w9, cs ; x9 = if carry { 0xffff_ffff } else { 0 }
add {result}, x9, x8 ; result = x8 + x9
To quantify the impact of the branch and cset tricks I measured all combinations for all the batch sizes. The optimum appears to be both tricks, except for N=16 where not doing tricks is beneficial.
\begin{array}{lrrrrr} & N\!=\!1 & N\!=\!2 & N\!=\!4 & N\!=\!8 & N\!=\!16 \\[0.4em] \texttt{none} & 297 & 538 & 854 & 1152 & 1354 \\[0.4em] \texttt{branch} & 336 & 596 & 965 & 1303 & 1209 \\[0.4em] \texttt{csetm} & 297 & 539 & 851 & 1141 & 1052 \\[0.4em] \texttt{branch+csetm} & 338 & 608 & 1005 & 1394 & 1209 \\[0.4em] \end{array}
Montgomery reduction
\begin{aligned} \mod{\frac{x}{2^{64}}}_p &= \frac{x + m ⋅ p}{2^{64}} &\hspace{2em} m &= \mod{- x ⋅ p^{-1}}_{2^{64}} \end{aligned}
In Montgomery reduction we add a multiple m of the modulus to create an exact multiple of 2^{64}. This is efficient to implement because we pre-compute \mod{-p^{-1}}_{2^{64}} and do math modulo 2^{64}. It's main downside is that we are computing \mod{\frac{x}{2^{64}}}_p instead of \mod{x}_p. This is (usually) less of a problem that it might seem because we can pre-multiply our numbers by a factor of 2^{64} to compensate. For Goldilocks it unfortunately interferes with the nice bit-shift roots of unity. The method works for inputs in the range [0, 2^{64}⋅p) and reduces to [0,p).
Winterfell uses Montgomery reduction and has two implementations of the REDC algorithm, a relatively straightforward one and a very optimized one due to Thomas Pornin (Por22 section 5.1):
fn mul_por22(a: u64, b: u64) {
let x = (a as u128) * (b as u128);
let (x0, x1) = (x as u64, (x >> 64) as u64);
let (a, e) = x0.overflowing_add(x0 << 32);
let b = a.wrapping_sub(a >> 32).wrapping_sub(e as u64);
let (r, c) = x1.overflowing_sub(b);
r.wrapping_sub(0u32.wrapping_sub(c as u32) as u64)
}
This compiles down to
mul x8, x1, x0
umulh x9, x1, x0
adds x8, x8, x8, lsl #32
cset w10, hs
sub x8, x8, x8, lsr #32
sub x8, x8, x10
subs x8, x9, x8
mov x9, #-4294967295
csel x9, x9, xzr, lo
add x0, x8, x9
An interesting basis for Montgomery reduction is 2^{192} because \mod{2^{192}}_p = 1 so there would get a plain reduction method without a transform on the arguments. It's also interesting to do a multi-precision Montgomery reduction in base b = 2^{32} because \mod{-p^{-1}}_{b} = -1 and p = [1, -1]. We could even combine both ideas.
Barrett reduction
\begin{aligned} \mod{x}_p &= x - q ⋅ p &\hspace{2em} q &= \floor{\frac{x}{p}} \end{aligned}
Where we approximate q with \hat{q} and do a small number of final additions/subtractions of p to make it exact. In Handbook of Applied Cryptography algorithm 14.42 the approximation taken is
\begin{aligned} \hat{q} &= \floor{\frac{x ⋅ μ}{2^{128}}} &\hspace{2em} μ &= \floor{\frac{2^{128}}{p}} = 2^{64} + 2^{32} - 1 \end{aligned}
This approximates \hat{q} ≤ q ≤ \hat{q} + 2 so at most two final subtractions are required to reduce the result to [0,p). This method is awkward in practice because it requires 128-bit multiplications.
We can do better! Starting with the exact formula and writing it in base b=2^{32} we get
q = \floor{\frac{x_3 ⋅ b^3 + x_2 ⋅ b^2 + x_1 ⋅ b + x_0}{b^2 - b + 1}}
we can use polynomial division in b to split off the integer part
q = x_3⋅b + x_2 + x_3 + \floor{\frac{\p{x_1 + x_2} ⋅ b + x_0 - x_2 - x_3}{b^2 - b + 1}}
This suggest the approximation \hat{q} = x_3⋅b + x_2 + x_3. It can be shown that the remaining fraction is <3 so the approximation error is at most 2. This is as tight as the above method but without the 128-bit multiplications.
But wait, there's more! We can continue the polynomial division and get a series expansion in b
q = x_3⋅b + x_2 + x_3 + \floor{\frac{x_1 + x_2}{b} + \frac{x_0 + x_1 - x_3}{b^2} + ⋯}
Looking at the sequence we can see that the first term is in the range [0,2) and the remaining terms are all smaller than b^{-1}. This suggests we take out the first term to improve our estimate of q.
\hat{q} = x_3⋅b + x_2 + x_3 + \floor{\frac{x_1 + x_2}{b}}
It is easy to verify that \hat{q} ≤ q + 1 so we have at most one reduction remaining. But this approximation satisfies the stronger bound x - \hat{q} ⋅ p < 2^{64}.
Unfortunately it does not satisfy \hat{q} ≤ q!
fn mul_a(a: u64, b: u64) -> u64 {
let x = (a as u128) * (b as u128);
let (x0, x1) = (x as u64, (x >> 64) as u64);
let (_, c) = x0.overflowing_add((x1 << 32) - (x1 >> 32));
let q = x1.wrapping_add(x1 >> 32).wrapping_add(c as u64);
x0.wrapping_add(q << 32).wrapping_sub(q)
}
cmn x8, x9, lsl #32
lsr x10, x9, #32
adc x9, x10, x9
sub x8, x8, x9
add x0, x8, x9, lsl #32
\hat{q}⋅b^2 = x_3⋅b^3 + x_2⋅b^2 + x_3⋅b^2 + x_1⋅ b + x_2⋅b + x_0 + x_1 - x_3
\hat{q}⋅b^2 = x_3⋅b^3 + x_2⋅b^2 + x_3⋅b^2 + x_1⋅ b + x_2⋅b + x_0 + x_1 - x_3
This suggests two orthogonal modifications we can make. We can do an overflow check on q and handle all 128-bit inputs and/or we can add a final reduction step to bring the result in [0,p).
fn mul_b(a: u64, b: u64) -> u64 {
let x = (a as u128) * (b as u128);
let (x0, x1) = (x as u64, (x >> 64) as u64);
let r: u64;
unsafe { core::arch::asm!("
cmn {x0}, {x1}, lsl #32 ; carry flag from x0 + x1 << 32
lsr {q}, {x1}, #32 ; q = x1 >> 32
adcs {q}, {q}, {x1} ; q += x1 + carry (and set carry flag)
add {r}, {x0}, {q}, lsl #32 ; r = x0 + q << 32
sub {r}, {r}, {q} ; r -= q
b.cc 1f ; branch if q did not overflow
mov {q:w}, #-1 ; q' = 0xffff_ffff
add {r}, {r}, {q} ; r += q'
1:
",
x0 = in(reg) x0,
x1 = in(reg) x1,
q = out(reg) _,
r = lateout(reg) r,
options(pure, nomem, nostack),
)}
r
}
Going further
A theoretical limit to throughput is the ability to compute the 128-bit product. On an M1 Max this takes a mul and umulh instruction. A single Firestorm core has two multiply units with a throughput of one cycle so a 128-bit product can be computed each cycle (the instructions are not fused). At 3.2 GHz this means a limit of 3.2 GE/s per core. The presented methods reach 1.7 GE/s per core.
Question. Do vector instruction provide a better alternative to compute the 128-bit product? See for example the AVX512 implementation from Polygon Zero.
Appendix
Proof of x - \hat{q}⋅p < 2^{64}
Given x ∈ [0, 2^{128}), p = 2^{64} - 2^{32} + 1, write x in base b=2^{32} as x = x_3 ⋅ b^3 + x_2 ⋅ b^2 + x_1 ⋅ b + x_0 and define \hat{q} = x_3⋅b + x_2 + x_3 + \floor{\frac{x_1 + x_2}{b}}. Now proof that
x - \hat{q}⋅p < 2^{64}
Start by expanding everything on the left hand side in base b
\p{\begin{aligned} &x_3 ⋅ b^3 + x_2 ⋅ b^2 \\&+ x_1 ⋅ b + x_0 \end{aligned}} -\p{x_3⋅b + x_2 + x_3 + \floor{\frac{x_1 + x_2}{b}}} ⋅ \p{b^2 - b + 1}
Expanding the terms…
\begin{aligned} x_3 ⋅ b^3 + x_2 ⋅ b^2 + x_1 ⋅ b + x_0 \\ -x_3 ⋅ b ⋅ \p{b^2 - b + 1} \\ -x_2 ⋅ \p{b^2 - b + 1} \\ -x_3 ⋅ \p{b^2 - b + 1} \\ -\floor{\frac{x_1 + x_2}{b}} ⋅ \p{b^2 - b + 1} \end{aligned}
…all the terms…
\begin{aligned} x_3 ⋅ b^3 + x_2 ⋅ b^2 + x_1 ⋅ b + x_0 \\ -x_3 ⋅ b^3 + x_3 ⋅ b^2 - x_3 ⋅ b \\ -x_2 ⋅ b^2 + x_2 ⋅ b - x_2 \\ -x_3 ⋅ b^2 + x_3 ⋅ b - x_3 \\ -\floor{\frac{x_1 + x_2}{b}} ⋅ \p{b^2 - b + 1} \end{aligned}
… leads to a lot of cancellations:
\begin{aligned} \cancel{x_3 ⋅ b^3} + \cancel{x_2 ⋅ b^2} + x_1 ⋅ b + x_0 \\ -\cancel{x_3 ⋅ b^3} + \cancel{x_3 ⋅ b^2} - \cancel{x_3 ⋅ b} \\ -\cancel{x_2 ⋅ b^2} + x_2 ⋅ b - x_2 \\ -\cancel{x_3 ⋅ b^2} + \cancel{x_3 ⋅ b} - x_3 \\ -\floor{\frac{x_1 + x_2}{b}} ⋅ \p{b^2 - b + 1} \end{aligned}
which leaves us with
\begin{aligned} x_1 ⋅ b + x_0 +x_2 ⋅ b - x_2 -x_3 \\-\floor{\frac{x_1 + x_2}{b}} ⋅ \p{b^2 - b + 1} \end{aligned}
To deal with that integer division, recall the identity with modular reduction
\mod{x_1 + x_2}_b = \p{x_1 + x_2} - \floor{\frac{x_1 + x_2}{b}} ⋅ b
So that we can rewrite the integer division as
\floor{\frac{x_1 + x_2}{b}} ⋅ b = \p{x_1 + x_2} - \mod{x_1 + x_2}_b
which results in
\begin{aligned} x_1 ⋅ b + x_0 +x_2 ⋅ b - x_2 -x_3\\ -\p{\p{x_1 + x_2} - \mod{x_1 + x_2}_b}⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}} \end{aligned}
Expanding the terms…
\begin{aligned} x_1 ⋅ b + x_0 +x_2 ⋅ b - x_2 -x_3\\ -\p{x_1 + x_2}⋅\p{b - 1} + \mod{x_1 + x_2}_b⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}} \end{aligned}
…expanding…
\begin{aligned} x_1 ⋅ b + x_0 +x_2 ⋅ b - x_2 -x_3\\ -x_1⋅b - x_2⋅b + x_1 + x_2 + \mod{x_1 + x_2}_b⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}} \end{aligned}
…and canceling
\begin{aligned} \cancel{x_1 ⋅ b} + x_0 + \cancel{x_2 ⋅ b} - \cancel{x_2} -x_3\\ -\cancel{x_1⋅b} - \cancel{x_2⋅b} + x_1 + \cancel{x_2} + \mod{x_1 + x_2}_b⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}} \end{aligned}
leaves us with
\begin{aligned} x_0 - x_3 + x_1 + \mod{x_1 + x_2}_b⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}} \end{aligned}
This gives us the identity
x - \hat{q}⋅p = x_0 - x_3 + x_1 + \mod{x_1 + x_2}_b⋅\p{b - 1}-\floor{\frac{x_1 + x_2}{b}}
To maximize this we set x_2 = x_3 = 0, x_0 = x_1 = b - 1. This is the global maximum because maximizes every positive term while setting every negative term to zero
\p{b - 1} - 0 + \p{b - 1} + \mod{\p{b - 1} + 0}_b⋅\p{b - 1}-\floor{\frac{\p{b - 1} + 0}{b}}
\p{b - 1} + \p{b - 1} + \p{b - 1}⋅\p{b - 1}
\p{b - 1}^2 + 2⋅\p{b - 1}
b^2 - 1
Proof of \hat{q} ≤ q
Not true. Take x_3 > 0 and x_0 = x_1 = x_2 = 0.
