The Goldilocks Prime

\gdef\delim#1#2#3{\mathopen{}\mathclose{\left#1 #2 \right#3}} \gdef\p#1{\delim({#1})} \gdef\abs#1{\delim\vert{#1}\vert} \gdef\F{\mathbb{F}} \gdef\mod#1{\delim[{#1}]}

In Ham15 Mike Hamburg introduced a class of primes of the form p = φ^2 - φ - 1 and named them Goldilocks primes. In those prime fields φ satisfies the Golden ratio relation φ² = φ + 1. When φ is a power of two this allows for very efficient implementation. Unfortunately, the -1 at the end means it will have very few power-of-two roots of unity. We'd like to have many so we can do big number theoretic transforms.

We will instead consider primes of the form p = φ^2 - φ + 1. Following the plonky2 project we keep the name Goldilocks prime. Now φ satisfies a modified Golden ration relation φ² = φ - 1. More importantly, the +1 at the end guarantees we will have a φ-th root of unity.

The values of φ and p where p is prime are the sequences A055494 and A002383 respectively:

\begin{aligned} φ &= 2, 3, 4, 6, 7, 9, 13, 15, 16, 18, 21, 22, 25, 28, …, \\ p &= 3, 7, 13, 31, 43, 73, 157, 211, 241, 307, 421, … \end{aligned}

As mentioned, in the prime field \F_p we have φ^2 = φ - 1. From this further useful relations on the powers of φ follow:

\begin{aligned} φ^3 &= - 1 &\hspace{2em} φ^4 &= - φ &\hspace{2em} φ^5 &= 1 - φ &\hspace{2em} φ^6 &= 1 \end{aligned}

And the pattern repeats. This shows hat φ is a primitive 6th root of unity. These relations leads to a particularly efficient modular reduction algorithm. First we write the number n in base φ:

n = n_0 + n_1 ⋅ φ + n_2 ⋅ φ^2 + n_3 ⋅ φ^3 + n_4 ⋅ φ^4 + ⋯

We get rid of all the terms n_{>3} by folding them into n_0, n_1, n_2 using the relations on φ^3 and φ^6.

\begin{aligned} n_0' &= n_0 - n_3 + n_6 - n_{9\phantom{0}} + ⋯ \\ n_1' &= n_1 - n_4 + n_7 - n_{10} + ⋯ \\ n_2' &= n_2 - n_5 + n_8 - n_{11} + ⋯ \\ \end{aligned}

To reduce this from three to two terms we use the relation on φ^2.

\begin{aligned} n_0' = n_0 - n_2 \\ n_1' = n_1 + n_2 \end{aligned}

The reduced number is n_0 + n_1 ⋅ φ. All that remains is carry propagation and some conditional subtractions of the modulus. Note that the reduction requires no multiplication operations.

To multiply two numbers a,b ∈ \F_p we can write them in base φ and make use of Karatsuba multiplication:

\begin{aligned} a⋅b &= (a_0 + a_1 ⋅ φ) ⋅ (b_0 + b_1 ⋅ φ) \\ &= a_0 ⋅ b_0 + (a_0⋅b_1 + a_1⋅b_0) ⋅ φ + a_1⋅b_1 ⋅ φ^2 \\ &= a_0 ⋅ b_0 - a_1⋅b_1 + (a_0⋅b_1 + a_1⋅b_0 + a_1⋅b_1) ⋅ φ \\ &= a_0 ⋅ b_0 - a_1⋅b_1 + ((a_0 + a_1) ⋅ (b_0 + b_1) - a_0⋅b_0) ⋅ φ \\ \end{aligned}

This requires three full multiplications in base φ and results in three terms. We reduce this to two terms using the final step of the modular reduction procedure.

Question. What do Barrett and Montgomery reduction look like?

A lucky binary base

To implement base φ operations efficiently we'd like it to be a power of two, i.e. φ = 2^k. There are not many such primes, the only solutions with k < 4000 are k = 1, 4, and 32. The first to are too small to be practically useful which leaves us with 32. φ = 2^{32} makes an especially useful prime p = 2^{64} - 2^{32} + 1 or written in full

p = 18446744069414584321 = \mathtt{0x\,ffff\,ffff\,0000\,0001}

This is a great size. It is small enough to fit in a 64-bit number, but large enough to do a lot of useful math in. For example, if we have three 32-bit numbers a,b,c ∈ [0, 2^{32}-1] we can compute a ⋅ b + c without overflowing:

a⋅b + c \enspace ≤ \enspace (2^{32} - 1)^2 + (2^{32} - 1) \enspace=\enspace 2^{64} - 2^{32} \enspace<\enspace p

When computing on 32/64-bit computers we have some useful interactions with the binary rings:

\begin{aligned} \mod{2^{n⋅32}}_p &= \mod{φ^n}_p &\quad \mod{2^{64}}_p &= \mod{-1}_{2^{32}} &\quad \mod{-p}_{2^{64}} &= \mod{-1}_{2^{32}} &\quad \mod{φ}_{2^{32}} &= 0 & \end{aligned}

The first identity gives us a very efficient way to implement bit-shifts. This in turn leads to an efficient inversion algorithm from the half-extended binary GCD:

def inverse(a):
    (u, a) = (MODULUS, a)
    (t0, t1) = (0, 1)
    twos = trailing_zeros(v)
    v >>= twos
    twos += 96 # 2^96 = -1
    while u != v:
        u -= v
        t0 += t1
        count = trailing_zeros(u)
        u >>= count
        t1 <<= count
        twos += count
        if u < v:
            (u, v) = (v, u)
            (t0, t1) = (t1, t0)
            twos += 96 # 2^96 = -1
    return t0 << ((191 * twos) % 192) # 2^-1 = 2^191, 2^192 = 1

Multiplicative group

The multiplicative group has order p - 1 and factors into a power of two and, interestingly, all five known Fermat primes.

p - 1 = 2^{32} ⋅ 3 ⋅ 5 ⋅ 17 ⋅ 257 ⋅ 65537

The factor 2^{32} means we can do efficient NTTs of power-of-two sizes using the Cooley-Tukey algorithm. The Fermat primes are not just curious, they allow us to use Rader's FFT algorithm to turn the Fermat prime sized NTTs into power-of-two NTTs. With efficient NTTs for all prime factors we can use the Good-Thomans algorithm to efficiently combine these without requirng twiddle factors. Overall this gives decent NTT performance for any divisor of p-1.

But what if we want a different size? The usual method is to pad the data until it is a power of two size. This is wasteful as can mean almost doubling the size. Instead we could go beyond powers of two and include the other small primes 3, 5 things improve quite a bit

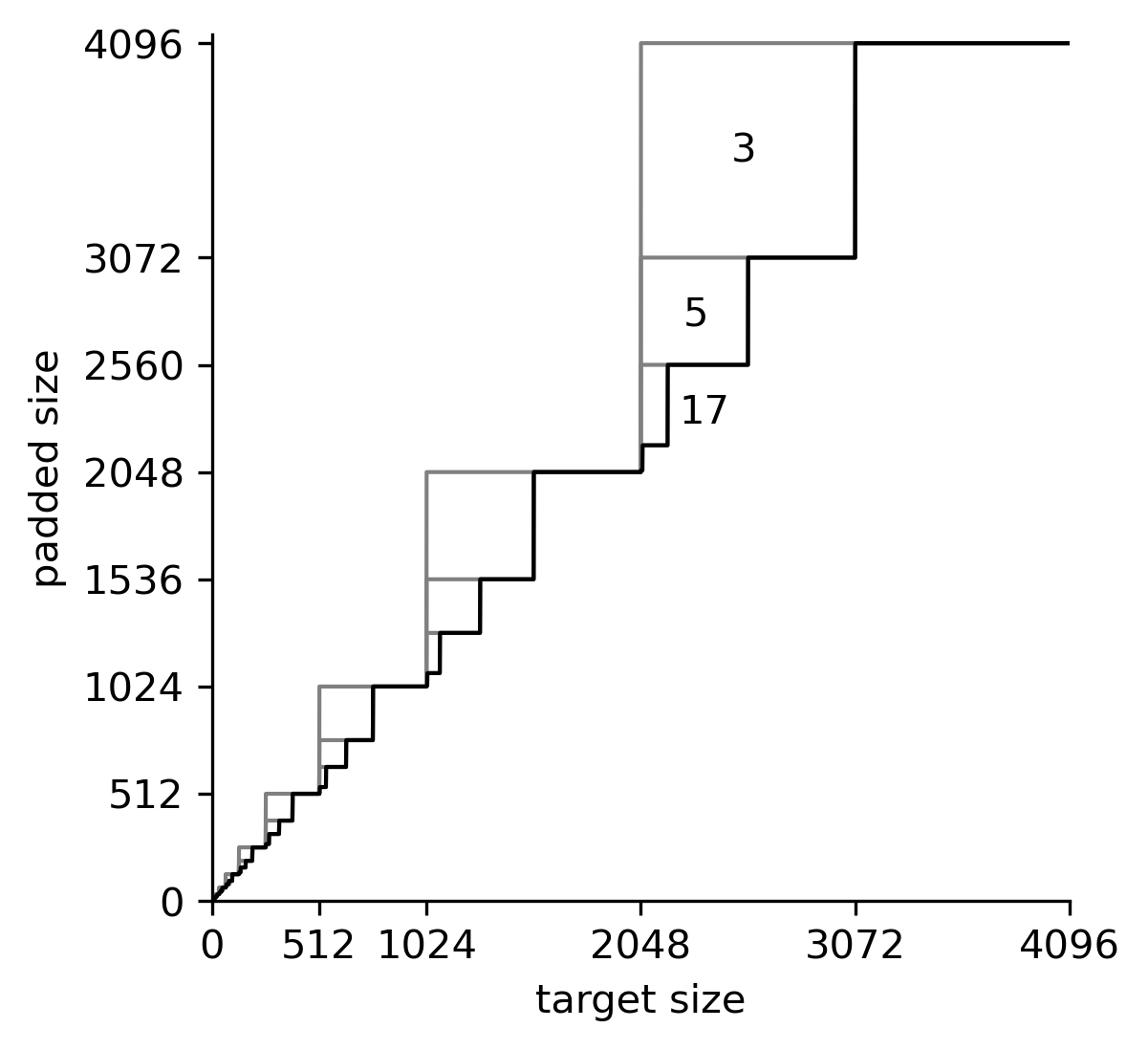
For example if we do a 2^{32} ⋅ 3 mixed radix, then in half of the cases it is 25% smaller than if we only use 2^{32}. If we also add 5 then in a quarter of the cases it is an extra 16% smaller. These two seem worthwhile. Adding 17 still gives a visible improvement, but is probably not worth the implementation complexity. And 257 and 65537 do not contribute anything noticeable.

NTTs require lot's of multiplications by roots of unity. Goldilocks again helps us make this efficient. We already found that φ=2^{32} is a 6th root of unity, and multiplying by it is simply a left shift of 32 bits. But if 2^{32} is a 6th root, then 2 itself must be a 6 ⋅ 32 = 192th root. Great! This means multiplying by 192th roots is just cheap bit shift. And since 192 = 2^6 ⋅ 3 has many divisors we can now create a whole set of n-th roots ω_n that can be implemented using bit shifts:

\begin{aligned} ω_2 &= 2^{96} & ω_{6\phantom{0}} &= 2^{32} & ω_{16} &= 2^{12} & ω_{48} &= 2^{4} & ω_{192} &= 2\\ ω_3 &= 2^{64} & ω_{8\phantom{0}} &= 2^{24} & ω_{24} &= 2^{8} & ω_{64} &= 2^{3} \\ ω_4 &= 2^{48} & ω_{12} &= 2^{16} & ω_{32} &= 2^{6} & ω_{96} &= 2^{2} \\ \end{aligned}

We can go even further and construct a 384th root using two bit shifts, but for that we need a trick. Schönhage observed that given an 8th root ω_8, the value ω_8 + ω_8^7 is a square root of 2. Let's quickly check this

(ω_8 + ω_8^7)^2 = ω_8^2 + ω_8^{7⋅2} + 2 ⋅ ω_8^{1+7} = ω_8^2 - ω_8^2 + 2 = 2

In Goldilocks 2^{24} is an 8th root and 2^{96} = -1 so n = 2^{24} - 2^{72} is a square root of two. Furthermore since n^2 = 2 and 2 is a 192th root, it follows that n is a 384th root ω_{384}. If we don't want that factor of 3 we can compute

ω_{128} = ω_{384}^3 = ω_{384}^2 ⋅ ω_{384} = 2⋅(2^{24} - 2^{72}) = 2^{25} - 2^{73}

This also shows that all even powers of ω_{384} have one bit set and all odd powers two.

ω_{384}^i = \begin{cases} 2^{k} & i = 2⋅k \\ 2^{k + 24} - 2^{k + 73} & i = 2⋅k + 1 \\ \end{cases}

This \sqrt{2} trick is useful, let's understand it better and see if we can take it further.

Schönhage's trick

To intuitively understand why this works, forget for the moment that we are working in a prime field and imagine the 8th roots of unity in the complex plane.

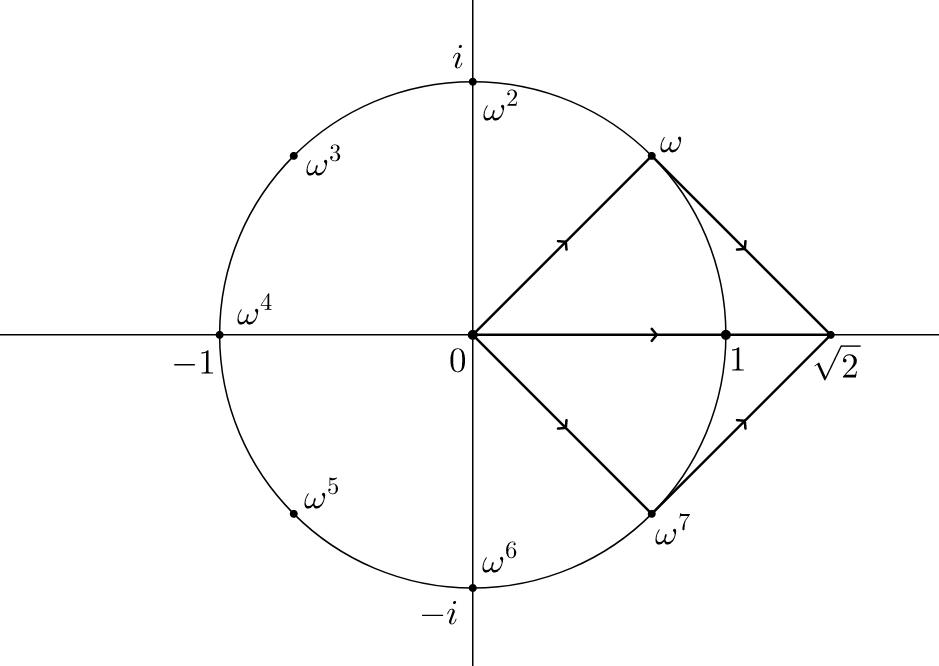
We can construct the sum ω_8 + ω_8^7 by adding vectors. Pythagoras theorem shows it is \sqrt{2}. This procedure generalizes this to n-roots with ω_n + ω_n^{n-1}, where the angles between roots are \frac{2⋅π}{n}. A bit of trigonometry shows the solutions

ω_n + ω_n^{n-1} = 2 ⋅ \cos \frac{2⋅π}{n}

For certain values of n there are simple exact values for \cos, see a table of exact trigonometric values. We indeed get \sqrt{2} and a few more. Most look quite uninteresting, but these two I like

\begin{aligned} % ω_{8\phantom{0}} + ω_{8\phantom{0}}^7 &= \sqrt{2} \\ ω_{12} + ω_{12}^{11} &= \sqrt{3} &\hspace{2em} ω_{10} + ω_{10}^9 &= \frac{1 + \sqrt{5}}{2} \end{aligned}

The last one is also known as the Golden ratio. It turns out these work in the Goldilocks field as well. Since ω_{12} = 2^{16} we have \sqrt{3} = 2^{16} - 2^{80}. For ω_{10} I don't know a multiplication free construction.

Question. It is possible to geometrically construct \sqrt[4]{2} using the geometric mean theorem. Is there a construction that leads to an efficient (multiplication free) implementation?

Adam P. Goucher explains that it is not possible to construct \sqrt[4]{2} as a rational function of roots of unity.

Generators

So far we've cleverly constructed roots up to ω_{384}, but for our NTTs we need all the roots up to the 2^{32}th. The standard way to do this is to find a generator of the multiplicative group. A generator is a field element g such that all non-zero numbers can be written as powers g^i for some i. There are many such numbers and the smallest generator in Goldilocks in 7. By Fermat's little theorem we have g^{p - 1} = 1 and thus g is a primitive (p-1)-th root of unity. Since this is the highest possible root of unity, we can derive all others from it using

ω_n = g^{\frac{p - 1}{n}}

It is convention to use the smallest generator, but if we compute ω_{192} with g=7 we get 35184372080640 instead of 2. This happens because n-th primitive roots are not unique and there are many choices that work. While this is still a power of two, ω_{192} = 2^{77}, it makes things more complicated than they need to be and we get a more complicated formula for ω_{384}^i.

A priory there is no reason to pick one choice of roots over the other. But we do need our choices to be consistent, meaning we want

ω_n = ω_{k⋅n}^k

to hold where applicable. Using a generator full fills that requirement. We'd also like a choice where we have an easy formula for multiplication by ω_{384}^i in terms of bit shifts. The smallest generator that satisfies this is 554. But this one has ω_{384} = -(ω_8 + ω_8^7), it takes the negative square root of two. The smallest generator that picks the positive root is 2717.

Question. Are there larger values of k for which 2^{2⋅k} - 2^k + 1 is prime or is 32 the largest?

Further references

• Gou21. Adam P. Goucher (2021). "An efficient prime for number-theoretic transforms".
• Po22. Thomas Pornin (2022).

https://github.com/mir-protocol/plonky2/issues/1#issuecomment-809323437