Optimizing transaction settlement
Alice, Bob and their lexicographic friends traded extensively. All off-chain of course. They now have the following obligations to settle:
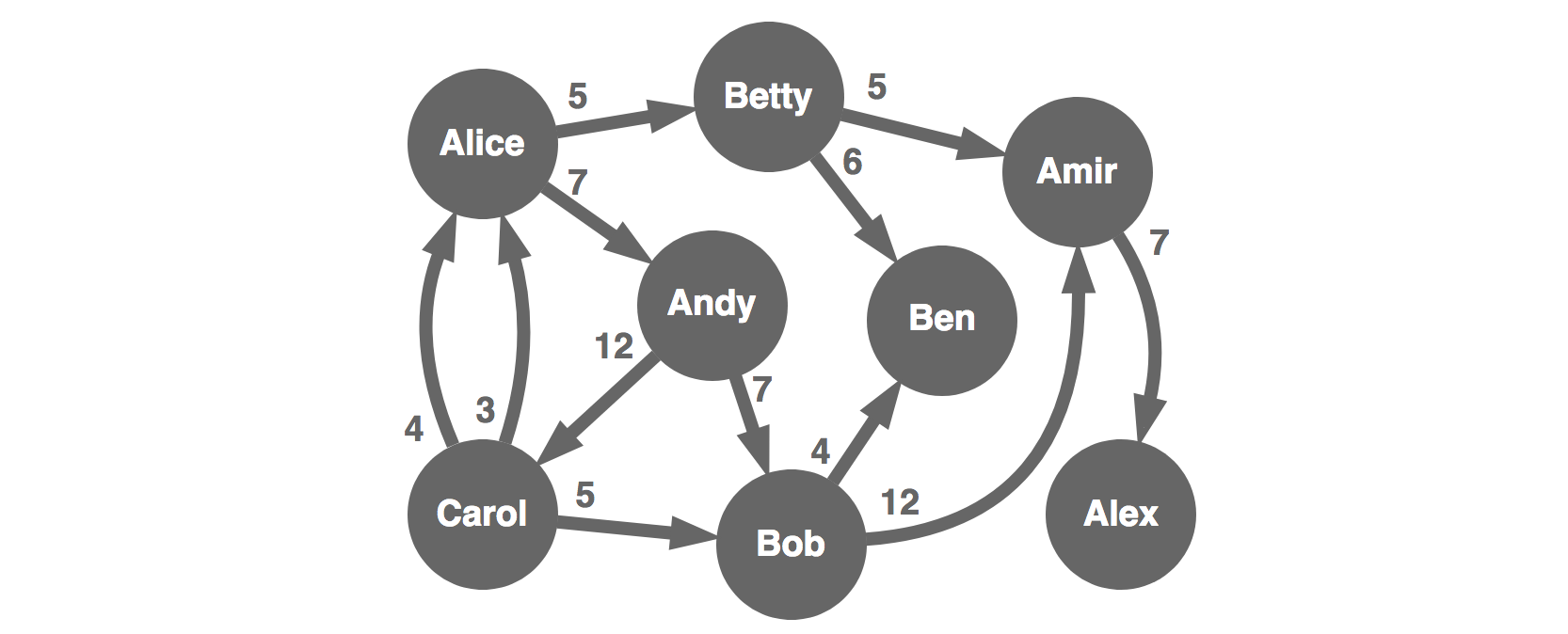
We can settle this as-is, with 12 transactions. But what is the smallest number of transactions required to settle these obligations?
(I’m going to present some intuitive tactics before getting to the optimal strategy. The impatient reader may skip ahead to ‘Solution’)
Tactics
Combine multi-edges

Whenever there are many transactions between two nodes, we can add them together. If transactions go in both directions, we subtract the smaller from the larger. This tactic reduces the number of transactions to at most n^2- n. It also means the optimal solution can not have multi-edges, so it must be a regular directed graph.
Cut loops
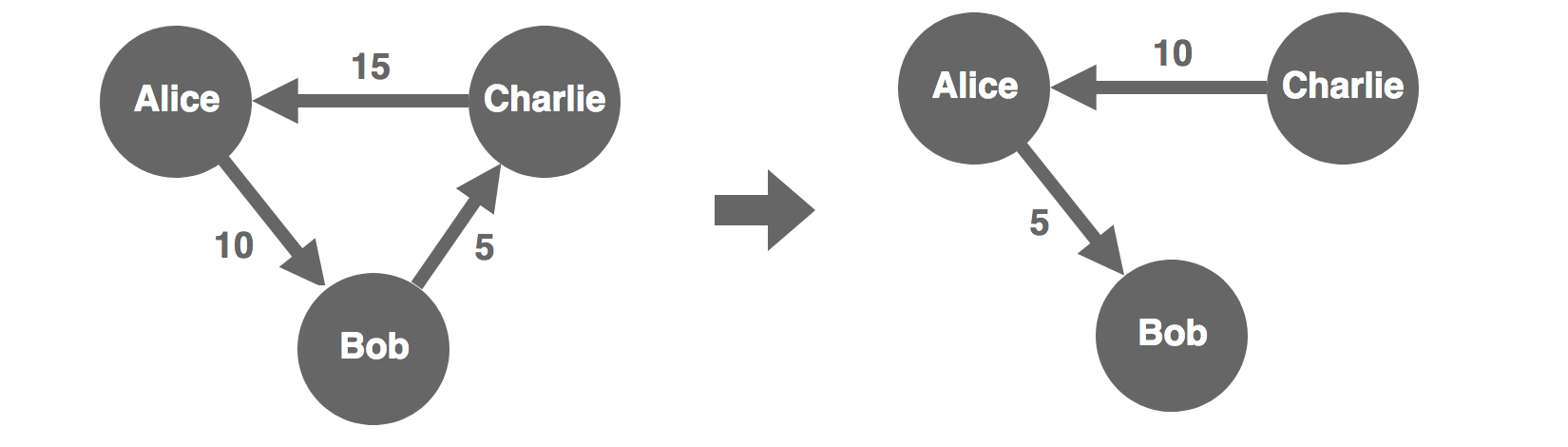
When there is a loop, we move money in a circle. We can add and subtract an amount to all the transactions in the loop and it would have no net effect. Take the smallest transaction amount and subtract it from the transactions. At least one transaction is now zero and the loop is cut. So the optimal solution must be loop free, an acyclic directed graph.
This also holds for undirected loops. We can pick a positive orientation for the loop and add or subtract an amount to cut the loop. So the optimal solution will have to be undirectionally loop free. In other words, the optimal solution will be a directed forest.
Of course, I will now show you a sub-optimal directed forest!
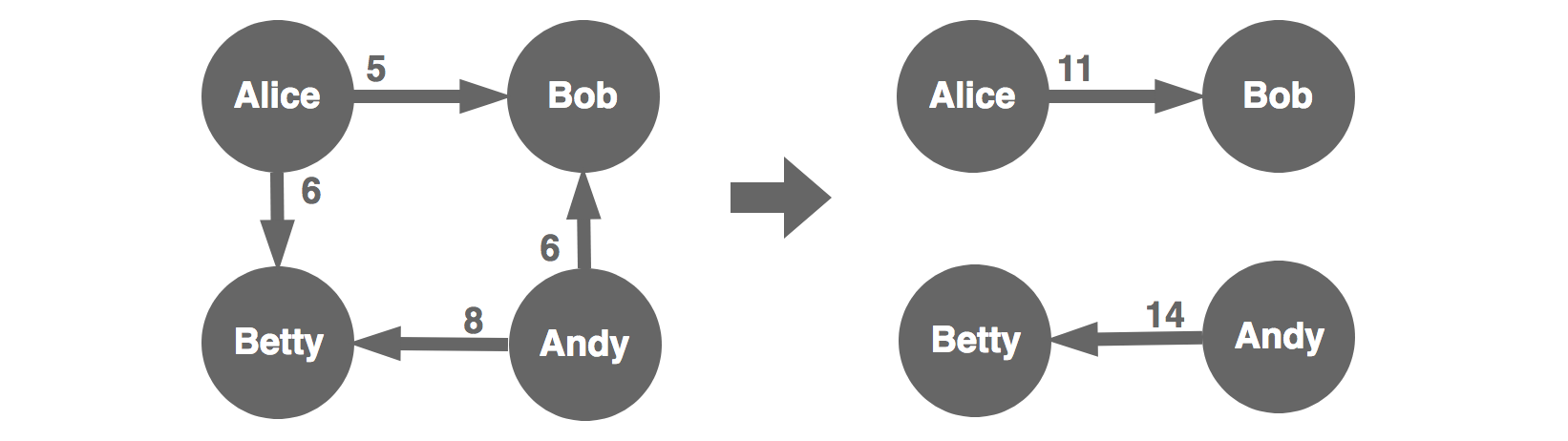
Remove pass-through nodes
Whenever a participant passes everything through, we can remove this participant and save a transaction. The general case of this does get quite a bit more complex, but there is always a solution:
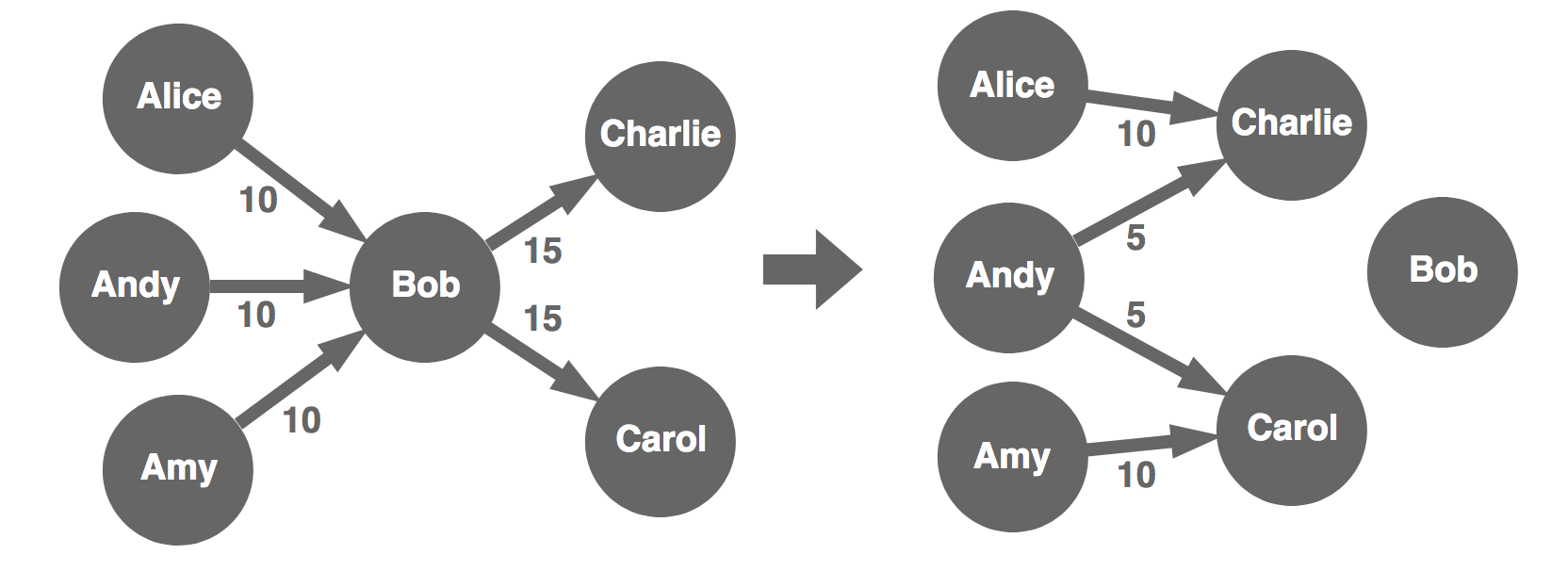
So the optimal solution will be a directed forest without pass-through nodes.
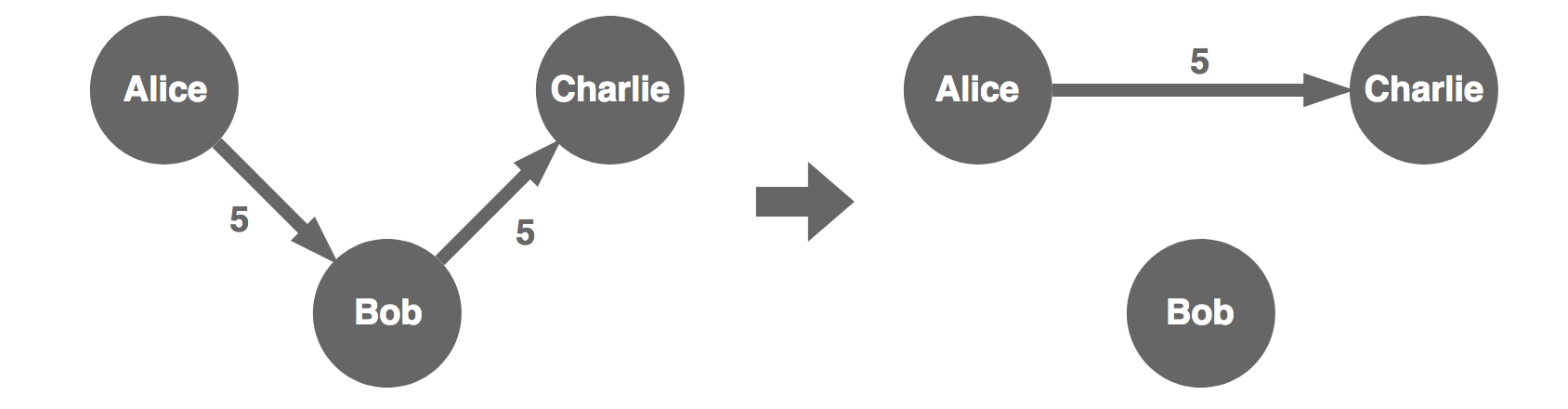
But what about this one:
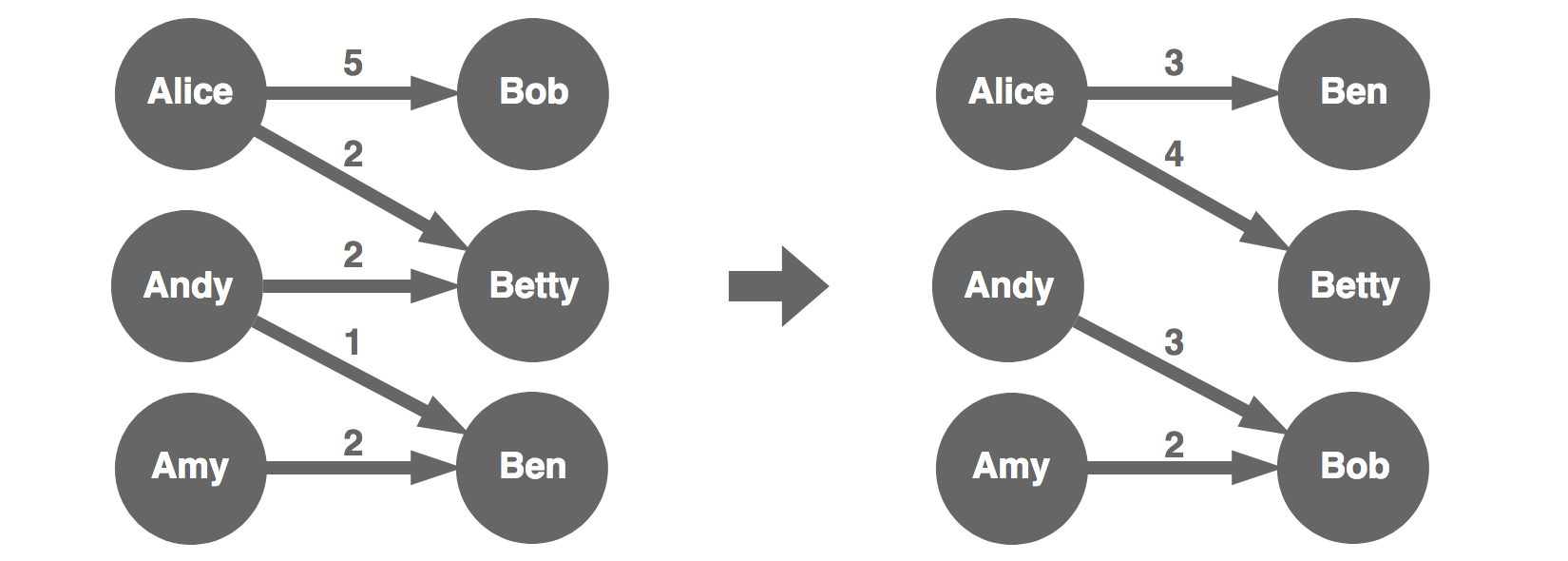
In the above, we switch the positions of Ben and Bob. We then adjust the transactions to make sure everyone pays and receives the same. In the process, one transaction disappears. We now have two trees in our directed forest instead of one. In a way, we did the same thing with the pass-through nodes, except we created a tree of one node. In a forest, we can not cut branches without creating new trees. So an optimal solution is a directed forest with the largest number of trees.
But how do we get there?
Solution
Compute the net change in balances
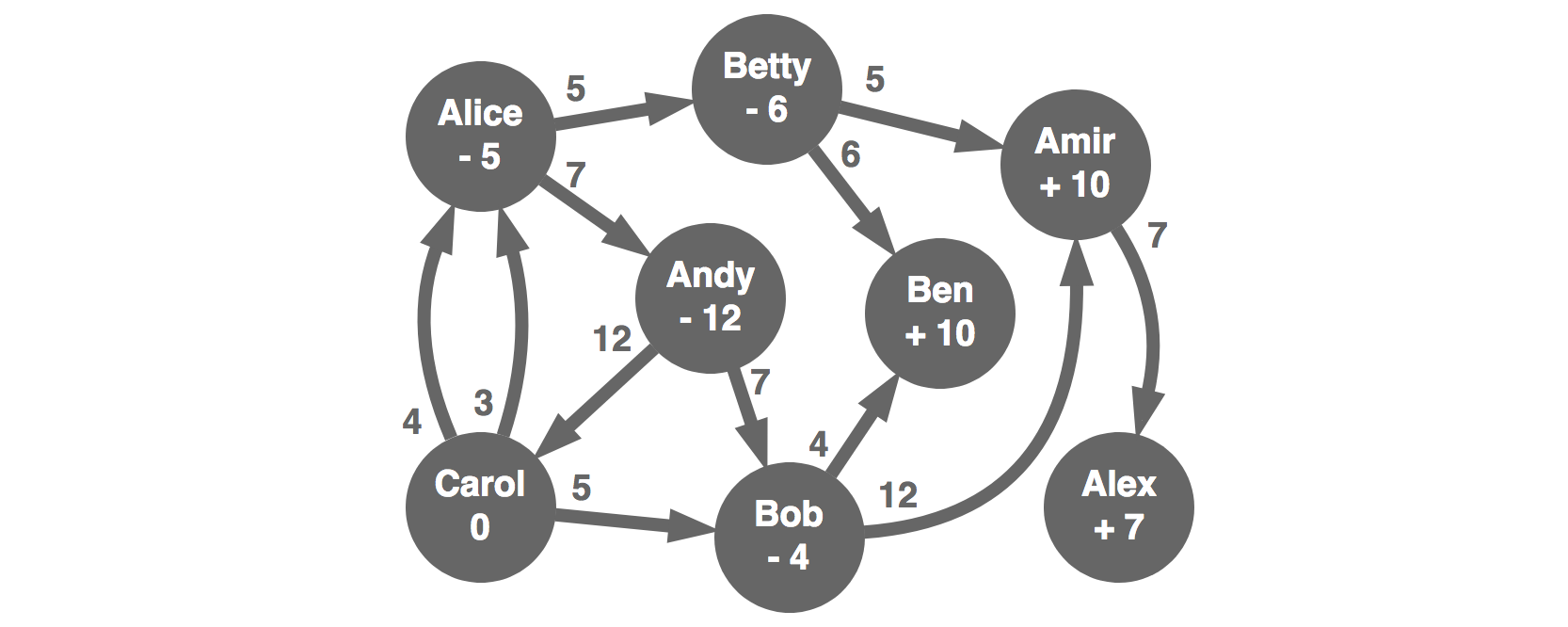
The net change in balances is all we care about. As long as these remain the same, we don’t care how we get there. So let’s forget about all the transactions. We will come up with a completely new set of transactions that has the same effect. The new transactions will be optimal by construction.
Also, observe that the sum of all the balance changes is zero. This is true because no money enters or leaves the system, we are only moving it around. Let’s try a divide-and-conquer approach. We split the problem into subsets that sum to zero, solve those and then combine those solutions into a global one.
Find groups that sum to zero
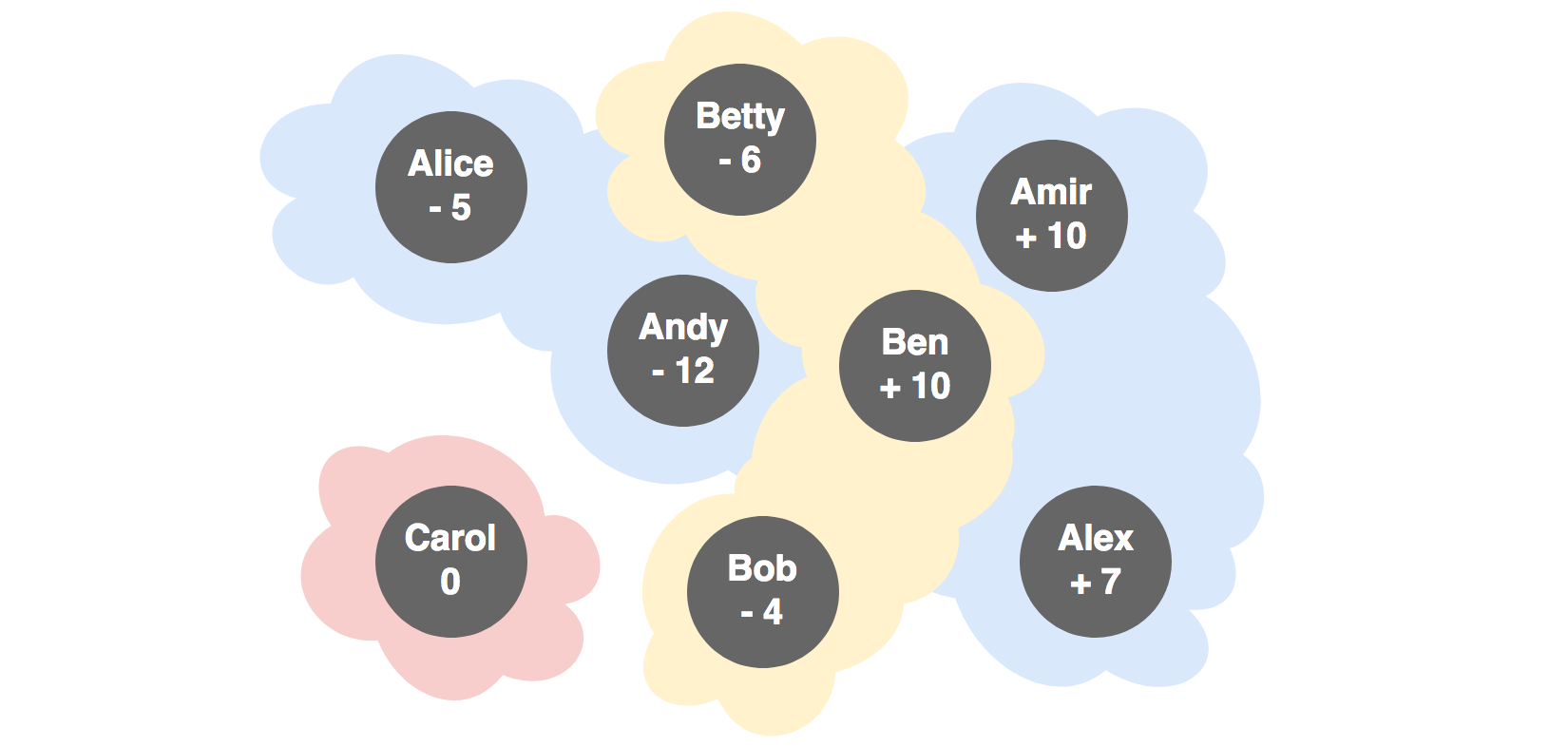
Finding these groups relates to the subset sum and the partition problem. These are NP-complete problems. It is difficult to find a set that sums to zero but easy to verify that it does. For the small values presented here, dynamic programming would work in reasonable time. For the 256-bit Ethereum balances, that won’t work. Brute force is a decent strategy for a small number of participants.
Now fun fact: NP-complete problems are perfect for Blockchain! Have users compute the solutions off-chain and post it along with the transaction. Then the smart contract can easily verify their correctness and settle the transfers.
We also don’t have to be too concerned with finding all subsets. We only save a single transaction for every zero set we find. If we don’t even look and take the set of all participants, that is still only n — 1 transactions, as we will see.
In practice, I expect two major sources of zero sets. First, pass-through accounts. Second, disjoint groups that do not transfer between each other. Balance changes summing to zero by coincidence seems unlikely.
Sort balance changes from large to small
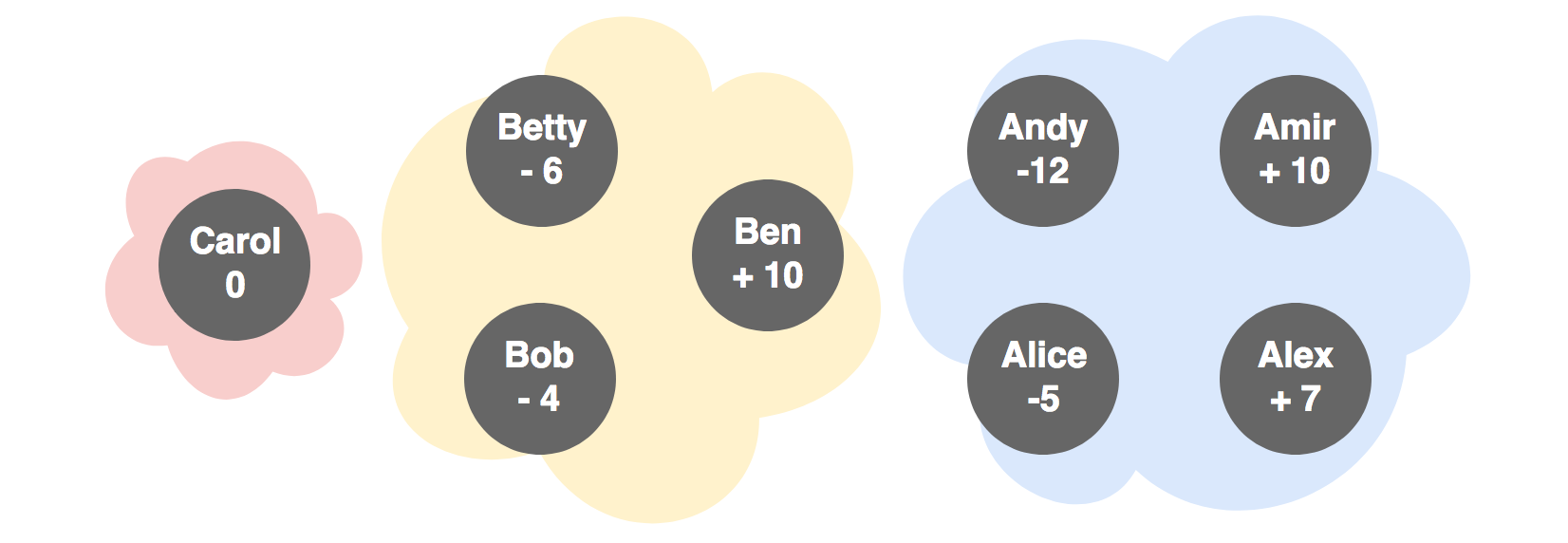
Sort each set in two columns, negative balances on the left and positive balances on the right. Sort the columns from large to small. Notice that the sum total of both columns is the same, but negated. We need to transfer money from left to right.
Create transactions top down
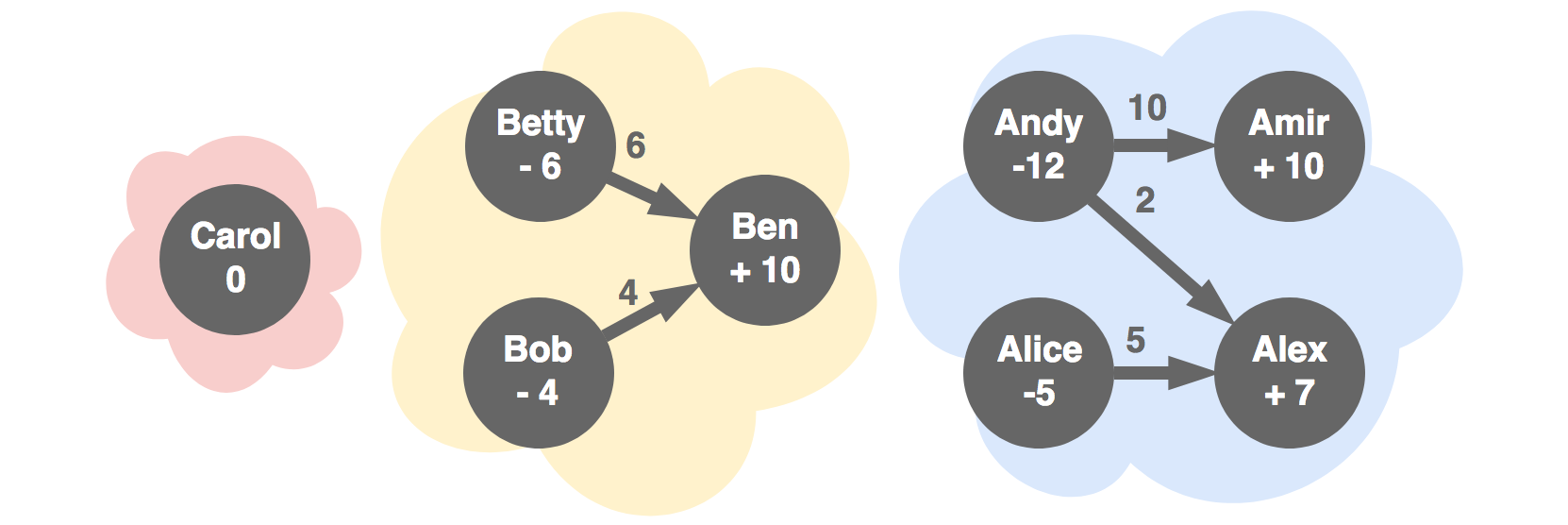
Start with the largest possible transaction between the top two nodes. Now exactly one of them will have its balance accounted for, it is out. Repeat the process for the remaining nodes, each time taking out one node. In the final transaction, both remaining nodes will finish, for a total of n — 1 transactions.
This is optimal.
Proof. We know that the set does not contain any strict subsets that sum to zero. Assume we can solve it with fewer than n - 1 transactions, this would create a transaction graph with n nodes and less than n - 1 edges. This transaction graph does not have enough edges to be connected and therefore has at least two disconnected components. These disconnected components individually sum to zero, which contradicts with there being no strict subsets that sum to zero. Therefore n - 1 transactions is optimal. ∎
Global solution
The union of these partial solutions is also the global solution. The total number of transactions is n - m where m is the number of zero subsets.
Proof. Assume there is a solution with fewer than n - m transactions. This solution graph must have more than m components. Each component has balances summing to zero, therefore there are more than m zero summing subsets. Contradicts our definition of m and therefore n - m transactions is optimal. ∎
Uniqueness
The solution is not unique, the following is also an optimal solution for the last subset:
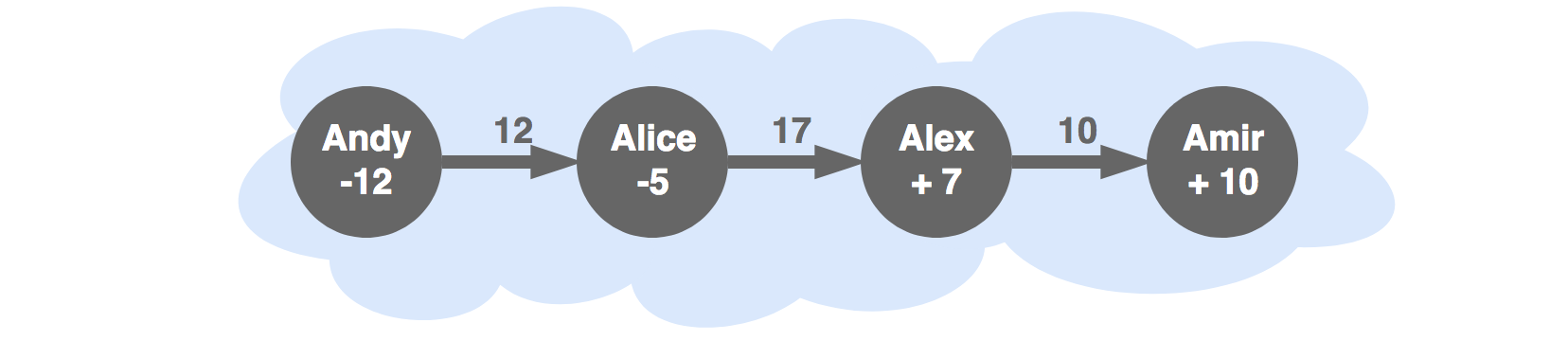
This solution is less desirable because it creates larger transactions. Larger than the net change in balance for the user. This can cause problems for accounts with transactions limits, such as ERC20 allowances.
It is also possible that there are many ways to partition the balances into m zero summing subsets.
The method presented above not only minimizes the number of transactions, it also distributes them evenly over the participants and minimizes the transaction volume. (Proof left as an exercise to the reader)
Despite a bit of searching, I could not find a similar problem in the field of graph algorithms or optimization. Literature references welcome!
