Even faster ζ(2n) calculation!
In the previous post I benchmarked several algorithms for computing $ζ(2n)$. All of them where, at some point, an improvement over the implementation in mpfr. At very high $n$ nothing seemed to come even near the series summation with recycled powers method, but this method is impossibly slow at the start. So we used Harvey’s method to bridge the gap.
I originally tried the von Staudt-Clausen method with the series
summation, but it preformed no different from the version with
mpfr_zeta_ui. Using von Staudt-Clausen with Harvey’s method is
pointless, since it already uses it internally. The last option, von
Staudt-Clausen with power table recycling series is also impossible, the
number of terms and precision required would increase with $n$, so the
whole table would have to be regenerated at every step.
And then the obvious struck me: the powtable method can be combined with von Staudt-Clausen if $n$ is decreasing! Evaluating the first terms of the Khinchin calculation backwards is not too hard and a quick test showed that von Staudt-Clausen has a considerable performance boost over Harvey’s method.
A nice consequence of this choice is that all the code is currently developed by ourselves, excluding the GMP, MPFR and C++ libraries, but those are mainly for simple arithmetic operations (simple as in the operations, not the implementation!) and input/output routines.
More efficient von Staudt-Clausen
The low precison $B_n$ was currently evaluated at high precision. But it only has to be accurate to a few digits after the decimal (binary?) point since we will be rounding it to integers. Let’s estimate its magnitude:
$$ \left\vert B_n \right\vert = \zeta(n)\frac{2n!}{(2 \pi)^n} < \left( 1 + \frac{2}{2^{n}}\right)\frac{2 \mathrm{e}^{n \ln n - n}}{(2 \pi)^n} $$
Now the number of bits required in $B_n$ is
$$ \log_2 \left( 1 + \frac{2}{2^{n}}\right) + 1 + (n \ln n - n) \log_2 \mathrm{e} - n \log_2 2 \pi $$
With a safety margin of 39 bits and an upper bound of 2 on the first log₂ this becomes:
$$ 42 + (n \ln n - n) \log_2 \mathrm{e} - n \log_2 2 \pi $$
Less bits in zeta
In the last half of the $n$ the $\zeta(2n)-1$ consists of a bunch of zeroes, a one, a smaller bunch of zeroes and then some interesting bits. The second set of zeroes takes up valuable computation time which can be eliminated by taking out the $\frac{1}{2^{2n}}$ term and implementing it separately using bit shifting. A nice consequence is that after a certain n there is no zeta calculation necessary anymore!
Source code
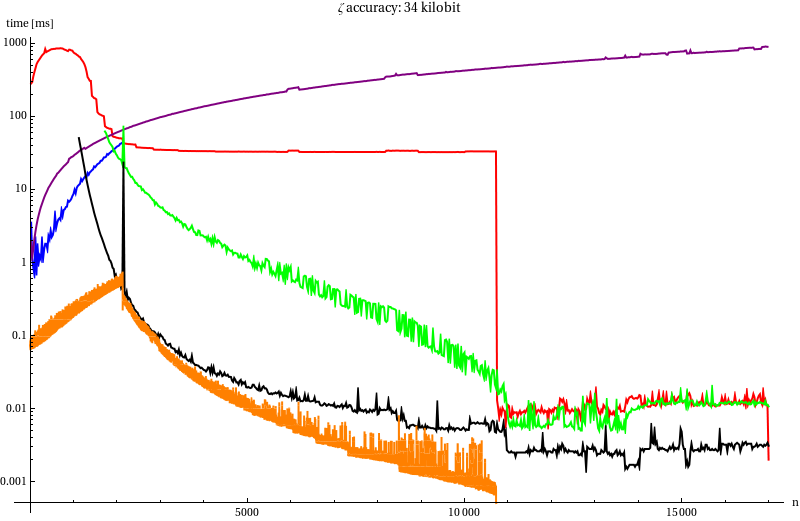
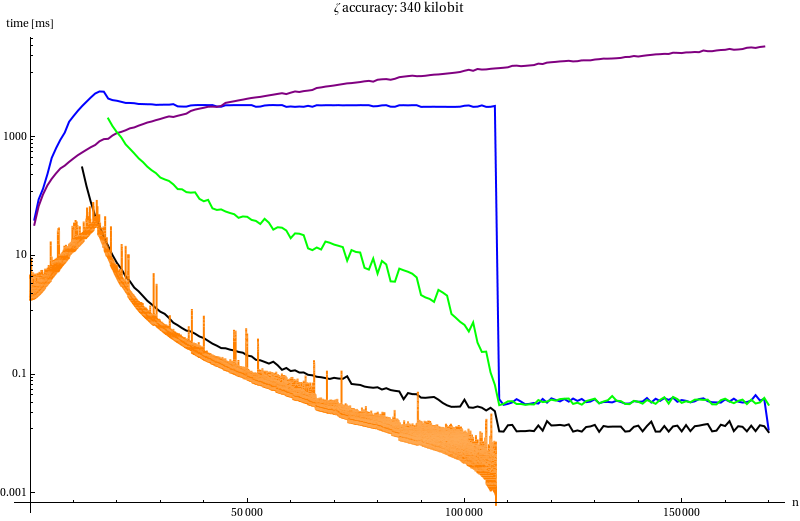
Benchmark
| Line | Method |
|---|---|
| Red line | mpfr_zeta_ui |
| Blue line | mpfr_zeta_ui with our von Staudt-Clausen |
| Purple line | Darvid Harvey’s bernoulli |
| Green line | Series summation without recycling |
| Black line | Series summation with power table |
| Orange line | Power table + von Staudt-Clausen |